Skip to contents

Project matrix after optimization

Source: R/project_matrix.R
project_matrix.Rd

After the MAP permutation was found with find_MAP(), use this permutation to approximate the covariance matrix with bigger statistical confidence.

Usage

project_matrix(S, perm, precomputed_equal_indices = NULL)

Arguments

S

A square matrix to be projected. The empirical covariance matrix. (See the S parameter in the gips() function). When it is not positive semi-definite, it shows a warning of a class not_positive_semi_definite_matrix.

perm

A permutation to be projected on. An object of a gips class, a gips_perm class, or anything that can be used as the x argument in the gips_perm() function.

precomputed_equal_indices

This parameter is for internal use only.

Value

Returns the matrix S projected on the space of symmetrical matrices invariant by a cyclic group generated by perm. See Details for more.

Details

Project matrix on the space of symmetrical matrices invariant by a cyclic group generated by perm. This implements the formal Definition 3 from references.

When S is the sample covariance matrix (output of cov() function, see examples), then S is the unbiased estimator of the covariance matrix. However, the maximum likelihood estimator of the covariance matrix is S*(n-1)/(n), unless n < p, when the maximum likelihood estimator does not exist. For more information, see Wikipedia - Estimation of covariance matrices.

The maximum likelihood estimator differs when one knows the covariance matrix is invariant under some permutation. This estimator will be symmetric AND have some values repeated (see examples and Corollary 12 from references).

The estimator will be invariant under the given permutation. Also, it will need fewer observations for the maximum likelihood estimator to exist (see Project Matrix - Equation (6) section in vignette("Theory", package = "gips") or in its pkgdown page). For some permutations, even \(n = 2\) could be enough. The minimal number of observations needed are named n0 and can be calculated by summary.gips().

For more details, see the Project Matrix - Equation (6) section in vignette("Theory", package = "gips") or in its pkgdown page.

See also

  • Wikipedia - Estimation of covariance matrices

  • Project Matrix - Equation (6) section of vignette("Theory", package = "gips") or its pkgdown page - A place to learn more about the math behind the gips package and see more examples of project_matrix().

  • find_MAP() - The function that finds the Maximum A Posteriori (MAP) Estimator for a given gips object. After the MAP Estimator is found, the matrix S can be projected on this permutation, creating the MAP Estimator of the covariance matrix (see examples).

  • gips_perm() - Constructor for the perm parameter.

  • plot.gips() - For plot(g, type = "MLE"), the project_matrix() is called (see examples).

  • summary.gips() - Can calculate the n0, the minimal number of observations, so that the projected matrix will be the MLE estimator of the covariance matrix.

Examples

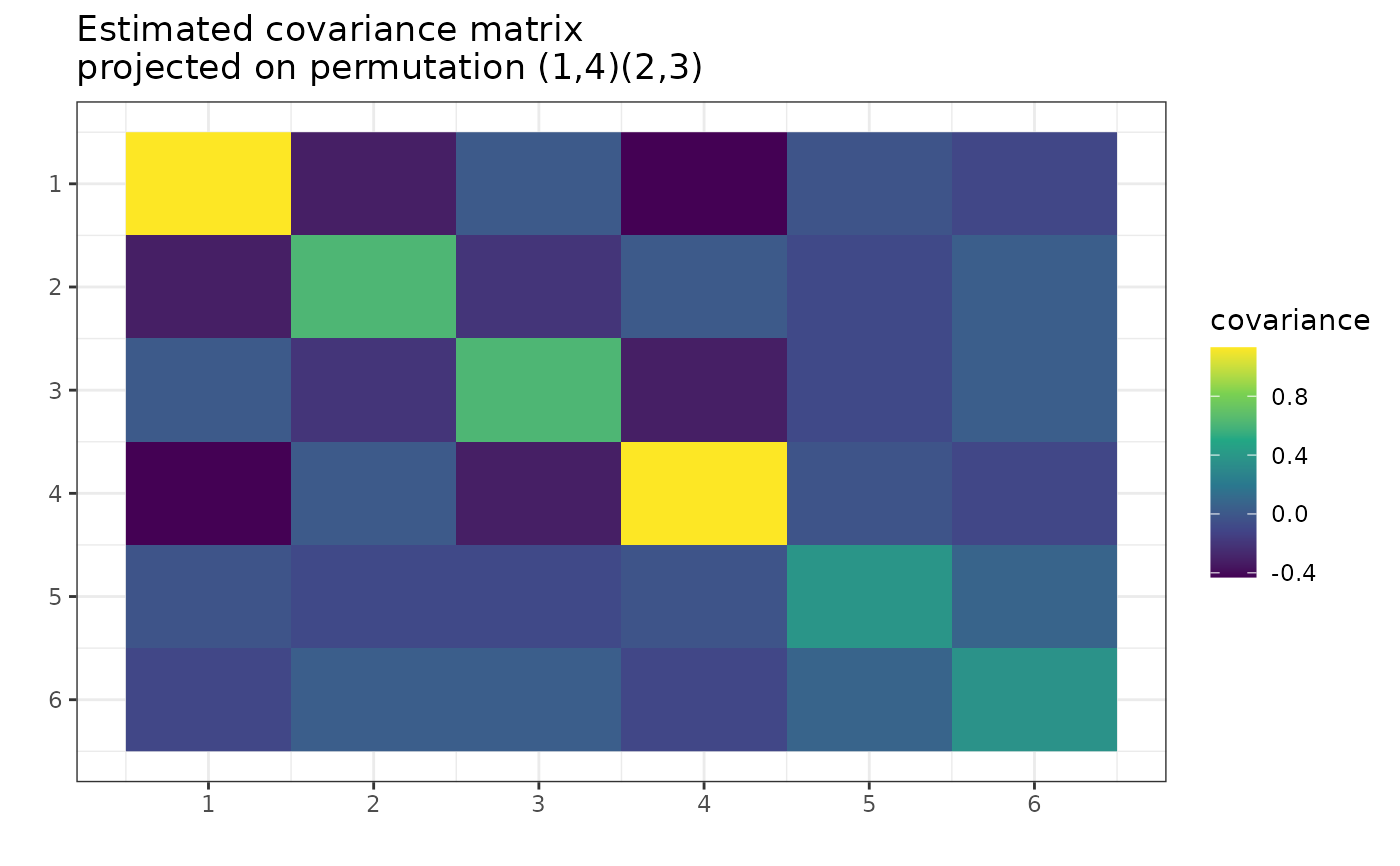
p <- 6
my_perm <- "(14)(23)" # permutation (1,4)(2,3)(5)(6)
number_of_observations <- 10
X <- matrix(rnorm(p * number_of_observations), number_of_observations, p)
S <- cov(X)
projected_S <- project_matrix(S, perm = my_perm)
projected_S
#>             [,1]        [,2]        [,3]        [,4]        [,5]       [,6]
#> [1,]  1.09598470 -0.06413469 -0.21185653 -0.43353246  0.05920705  0.2202124
#> [2,] -0.06413469  1.00959419  0.09589337 -0.21185653  0.48366779 -0.3530059
#> [3,] -0.21185653  0.09589337  1.00959419 -0.06413469  0.48366779 -0.3530059
#> [4,] -0.43353246 -0.21185653 -0.06413469  1.09598470  0.05920705  0.2202124
#> [5,]  0.05920705  0.48366779  0.48366779  0.05920705  1.15745710 -0.2385771
#> [6,]  0.22021240 -0.35300588 -0.35300588  0.22021240 -0.23857709  0.7438371
# The value in [1,1] is the same as in [4,4]; also, [2,2] and [3,3];
  # also [1,2] and [3,4]; also, [1,5] and [4,5]; and so on

# Plot the projected matrix:
g <- gips(S, number_of_observations, perm = my_perm)
plot(g, type = "MLE")


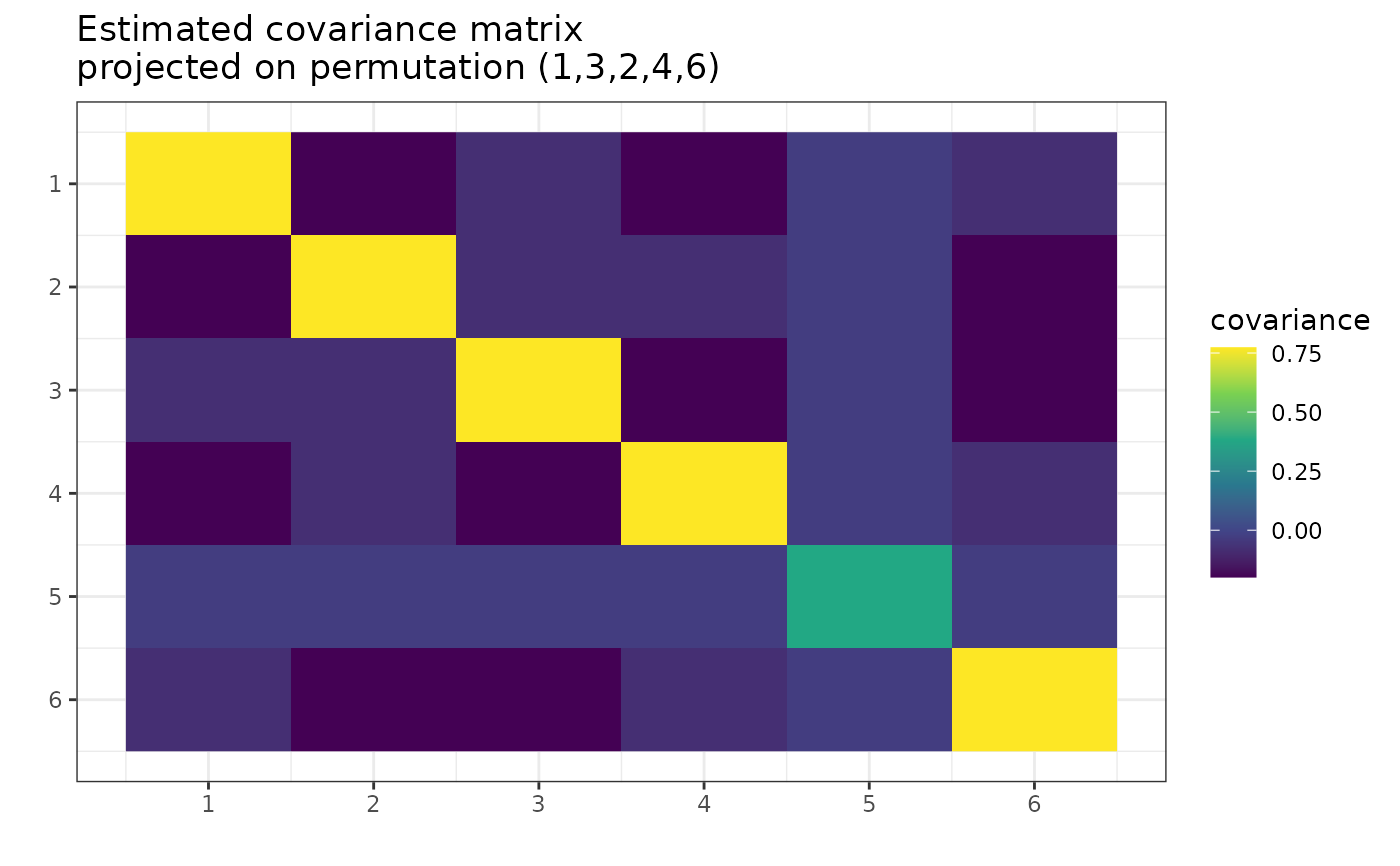
# Find the MAP Estimator of covariance
g_MAP <- find_MAP(g, max_iter = 10, show_progress_bar = FALSE, optimizer = "Metropolis_Hastings")
S_MAP <- project_matrix(attr(g, "S"), perm = g_MAP)
S_MAP
#>              [,1]        [,2]         [,3]         [,4]        [,5]
#> [1,]  0.686203184  0.06033489 -0.250237627 -0.009842726  0.06033489
#> [2,]  0.060334885  1.28496383  0.060334885 -0.317893688  0.74598323
#> [3,] -0.250237627  0.06033489  0.686203184 -0.009842726  0.06033489
#> [4,] -0.009842726 -0.31789369 -0.009842726  1.483914734 -0.31789369
#> [5,]  0.060334885  0.74598323  0.060334885 -0.317893688  1.28496383
#> [6,] -0.250237627  0.06033489 -0.250237627 -0.009842726  0.06033489
#>              [,6]
#> [1,] -0.250237627
#> [2,]  0.060334885
#> [3,] -0.250237627
#> [4,] -0.009842726
#> [5,]  0.060334885
#> [6,]  0.686203184
plot(g_MAP, type = "heatmap")